フーリエ級数の考え方から~前半~ [科学と技術一般]
フーリエ級数とは,任意の周期関数\(f(t)\)が,三角関数のサイン・コサイン波の足し合わせで表すことが出来るというものです。すなわち,
\[f(t)= \frac{a_0}{2} + \sum_{n=1}^{\infty}(a_n \cos{n\omega{t}} + b_n\sin{n\omega{t}} ) \tag{1}\]
と表すことが出来るとします。ここで,(1)式の係数 \(a_0\), \(a_n\), \(b_n\)は,それぞれ,
\[a_0= \frac{2}{T}\int_{-T/2}^{T/2} f(t)dt \tag{2}\] \[a_n= \frac{2}{T}\int_{-T/2}^{T/2} f(t)\cos{n\omega{t}} \tag{3}\] \[b_n= \frac{2}{T}\int_{-T/2}^{T/2} f(t)\sin{n\omega{t}} \tag{4}\] と表すことが出来ると*。ここで\(T\)は周期で,\(T=\frac{2\pi}{\omega}\)です。こういう表し方が可能ならば非常に便利です。音楽で考えれば,どんな楽器の音であっても,色んな高さのきれいな純音の足し算で出来上がっていると言えるわけです。\(n\)次高調波の考え方はこの表現から来ています。音程を示す基音は係数\(a_n\)および\(b_n\)の\(n=1\)の音,倍音というのは\(n\geqq2\)の音を言っている事に他なりません。弦楽器のハーモニクスというのも,まさにこれです。
嫌われる\(\sum\)記号を使いましたが,使わなければ,(1)式は, \[f(t)= \frac{a_0}{2} + a_1 \cos{\omega{t}} + b_1 \sin{\omega{t}} + a_2 \cos{2\omega{t}} + b_2 \sin{2\omega{t}}+ a_3 \cos{3\omega{t}} + b_3 \sin{3\omega{t}} + \cdots\]
という事です。ちなみに\(b_0\)は\(\sin{0}=0\) ですから,もともとゼロです。
ともあれ,なぜこんなことが出来るのでしょうか?
今ならパソコンのアプリなどで波形を描いてみれば,確かにそうなっているのを簡単に確認できます。これを習ったころは,電算機と言えば汎用機でしたから,FORTRANでプログラムを組んでカードを打ってプロッタなどを動かせばできなくはありませんでしたが,やはりそんな事をやっていたら落第していました(しかけてはいましたが)。
◆
ポイントは三角関数同士の直交性です。
図形の直交なら見たままですが,三角関数の直交性というのは,周波数が整数倍異なる関数同士を掛け算して一周期分定積分するとゼロになると言う性質です。これは積分を使わなくても,図形的に理解することも出来ます。
例えば,\(\sin{\omega{t}}\)と\(\sin{2\omega{t}}\)を掛け算すると,
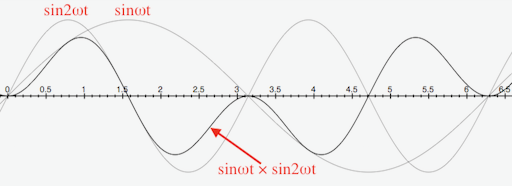
.png)
sinとcosの掛け算でも,やはり積分を使わずに図形的に見ても三角関数の公式(倍角公式)から周波数2倍のsin波となりますから,面積は上下で±ゼロになるのが分かります。
\[\sin{\omega{t}} \times \cos{\omega{t}} = \frac{1}{2} \sin{2\omega{t}}\] 周波数が整数倍異なるsinやcos同士を掛け算して一周期積分するとゼロになります。周波数が同じでもsinとcosはそうです。結局全部ゼロになっらたら何の意味もない事ですが,唯一ならないものがあります。
「それ自身」です。以下はその様子を図示したものです。
.png)
\[\sin{\omega{t}} \times \sin{\omega{t}} = \sin^2{\omega{t}} = \frac{1}{2}(1-\cos{2\omega{t}})\] (3)式(4)式につく係数2は,「それ自身」をぴったり1にするためです。
いずれにせよ,この三角関数の直交性は,未知の周期関数に含まれる「それ自身」を選り出すという,強力な「ふるい」になるわけです。どんなにデタラメな周期波形\(f(t)\)であっても,それに\(\cos{n\omega{t}}\)を掛け算した関数の一周期分の積分値を求め(て2倍す)れば,\(f(t)\)に含まれる\(\cos{n\omega{t}}\)の分量が分かり,同様に\(\sin{n\omega{t}}\)でやれば\(\sin{n\omega{t}}\)が含まれる量が分かるという,実にうまい仕組みです。
(1)から(4)式までの表し方は,最も初等的な書き方ですが,具体的な波形の計算をするには便利です。最初に必ずやるのが,矩形波の計算です。sin波的(奇関数)であれば,求める係数は(4)式の\(b_n\)のみで,求めた値を(1)式に戻すことになります。途中計算を省略しますが,矩形波のフーリエ級数表現は,以下の様になります。
\[f(t)= \frac{4}{\pi}\sum_{m=1}^{\infty}\frac{\sin{(2m-1)\omega{t}}}{2m-1}= \frac{4}{\pi} (\sin{\omega{t}} +\frac{1}{3}\sin{3\omega{t}}+\frac{1}{5}\sin{5\omega{t}} +\frac{1}{7}\sin{7\omega{t}} + \cdots )\] 下図は,これを図示したものです。
.png)
直流を単純にスイッチングして作った矩形波交流には3次,5次,7次などの奇数次高調波がたっぷりと含まれることがわかります**。自分で計算してみれば,例えばスイッチングのタイミングを少しずらすことで,一番大きな第3次を落とすことも可能だという事なども分かります。
奇数次高調波と言うのは,音で聴くとクラリネットの音色に近いものです。これは片閉じ管で発生する定在波振動を示しています。
矩形波は最初の一例になりますが,三角波でものこぎり波でも,それらのフーリエ級数を手計算することが出来ます。
もともとはこの手法は,フーリエが電熱解析用に開発したものですが,非常に応用範囲の広いもので,上で挙げた例の他,弦の振動はもちろん,量子力学のシュレディンガー方程式すら解くことが出来ます。上で見た様に三角関数の直交性というシンプルな性質を用いた驚異的な解析技法と言えます。これは,数学理論と言うよりも,各種分野に利用されて何ぼのものです。
(1)~(4)式は具体的な計算に使うには便利ですが,見た目はあまりよくありません。
例えば,\(a_0\)だけわざわざ分けて書いています。電気工学的にはこの項が「DC成分」を表し,その他の「AC成分」と区別できるわけですが,(1)式は「元の波形\(f(t)\)が三角関数波の重ね合わせで表される。」という意味で,(2),(3),(4)式はその重み;いわば周波数スペクトルを表している事になり,本来は(1)式と(2),(3),(4)式のセットとが対応する式になるはずですが,1対3ではその対応が悪いのです。
そこで登場するのが,やはり「オイラーの公式」です。これを用いればもっとすっきりとした書き方で表すことができます。
*電気信号や音などの時間波形を想定して時間\(t\),角周波数\(\omega\)を用いています。物性論や光学,画像解析などに用いる際は,距離\(x\), 波数(空間周波数)\(k\)などとします。
**矩形波のフーリエ級数は\(\frac{1}{n}\)の収束なので,インパルス波を除けば収束は遅い(高調波をタップリ含む)方です。四角い波形を丸っぽい正弦波で表すのですから,当然と言えば当然でしょう。例えば三角波は\(\frac{1}{n^2}\)で直ぐに収束します。




記事に関係のないコメントで恐縮です。
一時的に復活した拙ブログへのコメント、本当にありがとうございました。
by U3 (2023-02-02 14:05)
U3さん、
再コメさせていただきました。
by Enrique (2023-02-02 18:57)
感謝に堪えません!!
by U3 (2023-02-05 21:37)
U3さん、どういたしまして。
お陰様で見えて来たものもありますね。
by Enrique (2023-02-07 11:02)