音律を考える（3）「１オクターブには幾つ音がある？ピタゴラス律の場合」

音律に関する話の基礎事項をうだうだ書いています。

今回はピタゴラス律で，１オクターブ内にはどれだけの数の音があるのかを考えて見ます。

そんなの12音に決まってる！と，それでは話は終わってしまいます。

ピタゴラス律では3倍の系統（純正５度）のみで音階を作っていきます。もちろんオクターブは2倍です。2と3は素数で，お互い同士それぞれの倍数で表わすことができません。純正5度の倍数は3/2です。これを重ねていきます。最初が１，次が3/2，その次が9/4，27/8などと重ねていきます。純正5度上げるというのは，「5度圏時計」の短針を（ほぼ）１時間分進める事に相当します。

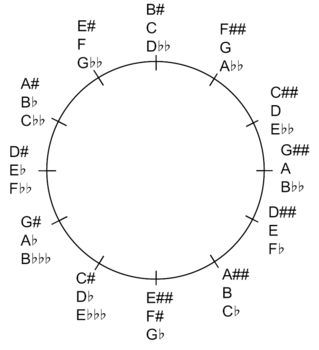
C 音からスタートしますと，対応する音はG, D, A, E, B(H), F#(Fis), C#(Cis), G#(Gis), D#(Dis), A#(Ais), E#(Eis), B#(His) などとなります。こうするのがピタゴラス音律式の音階音の作り方なのですね。ただし，実際には音は何オクターブにもわたりますから，オクターブ内に収めるため適宜2で割り算します（この比率の表を実際に用いられるピッチになるよう倍数を掛ければ実際に使う音階の周波数になります）。なので最後は，B# = (3/2)^12/(2^7)となります。ちなみに，最初の5音をとった（0時から始めて4時まで）のが5音音階（Ceciliaさんのライヤーがそうでした。調的なヴァリエーションありますが）であり，7音とった（11時から始めて5時まで）のが全音音階ですね。

エンハーモニック音を含む５度圏（右回りが#系で左回りが♭系）

右回り，左回りとも約1回転半ずつ書き込みましたが，これがすべてではなく後は幾らでも無限に続きます。

でも待てよ，最後のE#とかB#って何ですか？これらってFとかCとか言うんじゃ？

だって，ピアノの鍵盤のEの右にも，Bの右にも黒鍵はありません。あるのは，FとかCの白鍵だけじゃないですか？

まあ，そう割り切ったのが12平均律（ですし各種ウェルテンペラメントも近似的にはそう）なのですね。これを異名同音(Enharmonic Equivalent)とか言って，E#＝Fとか，B＃＝Cとしちゃうんですね。

しかし，平均律でなくピタゴラス律では，B#>Cです。正確には，B#= C + p.c.　となって約1/4半音程も高くなってしまうのですね。しかしこれは，何もピタゴラスのせいではなく，当時は半音階までの沢山の音を使わなかったのが，2000年も後の中世になって鍵盤楽器の発達に伴い問題になったようですね。

♭系では，C, F, B♭(B), E♭(Es)などと，左回りに行きます。やはり適宜オクターブ内におさめながら2/3倍していきます。左回りでも出発点に戻ってきたと思いきや，p.c.分行き過ぎるため，今度はその分音が低くなることになります。今度は，D♭♭= C - p.c.　なのですね。

なお，このピタゴラスコンマp.c.の値は，先日の記事でも示した通り，

p.c.=(2/3)＾12/2＾7＝1.013643265

です。セント値で言うと，23.5セントほどです。

このように，ピタゴラス音律では，シャープ系（右回り）では音が高くなり，♭系（左回り）では低くなります。これらの5度回転は，オクターブを越えても，F##, C##, G##などと，どんどん異名音を発生しながら進みます。左回りでも同様に♭系の異名音を発生しながら進みます。このことは，kotenさんの記事に詳しく書かれています。

オクターブを12回の純正5度の回転，すなわち，オクターブ内を12の音でやっつけてしまおうとすると，ピタゴラスコンマという，ずれを生んでしまいます。これは上で書いたように，原理的にどうしようもないものです。オクターブの系統すなわち2と，純正5度の系統すなわち3とは，互いに素数同士ですから，片方の値を積み重ねでもう片方の値を表すことは決して出来ません。すなわち，ぴったりいくことは決して無く，オクターブ内の音は無限にあることになるわけです。

無限ではどうしようもないので，ならば，オクターブ内をもっと細かくとったら精度はよくなるだろうという発想が出てきます。やってみますと，(3/2)の53乗が31オクターブ上で，元の音をわずかに通り過ぎています。

(3/2)＾53=2151972563

2＾31＝2147483648

で，両者の比率は1.002090314です。この新たな53ピタゴラスコンマは，セント値でいうと約3.6セントになります。

すなわち，E####### ＝C + 3.6セント です。　　

E#######って普通に考えるとB(H)ですから，いわば#高が積り積もって半音分食っちゃった！ということです。ピタゴラス音律の#7つ分は，およそ，8半音分くらいということですね。

この方法で作った音階はオクターブが53音で構成されることになります。エンハーモニック音が沢山出て面倒くさいですが，これで作ったピタゴラス音階と平均律音階のずれは，3.6セントの53分割ですから，ひとつの5度間隔につき0.07セントほどのずれになります。この53ピタゴラス律と53平均律の誤差はかなり小さく，過去にはこの53平均律を使ったオルガン等試作されたようですが，これは演奏できません。音の響き的には良好でしょうが，全く普及しなかったようです。

さて，もう少しイタズラをしてみましょう。次の元の音に近づくニアミスポイントはどこでしょうか？ちょっとプログラムで調べてみますと，

306回の5度回転で179オクターブをやや通り過ぎ，1.8セントと出ます。ここまで来ても大して精度上がりませんね。

お次は665回の5度回転，389オクターブ上で，0.076セントです。おーっ，急激に精度が上がりました。もちろん，全く実用性はないですが。このオクターブが665音で構成される，665ピタゴラス律と665平均律のずれは，一挙に10,000分の1セントほどになります。

これより精度の良い一致は，1000オクターブ以内には無いようです。

今日の結論

ピタゴラス音律式の方法では，1オクターブ内の音は原理的に無限にある。そこから重要な5音や7音，12音を拾って実用的な音階にしている。その際♯系が♭系よりも高くなる異名異音を発生する。53音，306音，665音なども理屈上では考えられる。

次はミーントーン音律について考えてみたいと思います（つづく）。

---

注記：

ちょっと気になったので付け加えます。本を読まない人間なもので。

「ピタゴラス音階の半音はリンマと呼ばれ，平均律の半音よりも狭い。」と書かれているものがあります。このリンマと呼ばれるものは，ピタゴラスコンマ分短くなった半音のことで，ここで取り上げている5度の集積でできる半音は，「ピタゴラスの長半音」とか呼ばれるようです。ピタゴラス律には半音が2種類あります。

コメント 4

Enriqueさん、kotenさん、REIKOさんの記事で勉強させていただいています。ひとつひとつ理解しようと思うと読むだけでとても時間がかかります。（笑）大体何となくですがわかりました。
ものを整理していたら最初に購入した電子ピアノの説明書が出てきました。純正律やピタゴラス音律で弾けることは覚えていましたが、中全音律、ヴェルクマイスター第Ⅲ法、キルンベルガー第Ⅲ法もできたということを知りました。しかも平均律も「調律曲線を使わない平坦な平均律」と「電源オン時のピアノ調律曲線に沿った平均律」の二種類ありました。
今思うと、それらを充分に味わえばよかったですね。もう手元にないので残念です。
by Cecilia (2011-01-18 08:32) 

Ceciliaさん，nice&コメントありがとうございます。
私の記事は，試していないので，ぜんぜん実践的でなくて，基礎の部分のみですが，ご理解の足しになれば良いかなと思っていますが，自分自身書いてみると良く分かっていないところやあいまいなところにも気づきます。ピタゴラス音律は3/2を重ねるだけなのでシンプルだと思いますが，理系の人間では当たり前と思って，はしょっているところもあるかもしれません。
オクターブは音の高さが２倍とか，普通はC音から始めるのに，ピッチはA音で決めるとか，５度音程は音の高さが3/2倍とか。。。
少し書き足しましたので，不明点あればご確認ください。なお，53平均律以降は私の趣味で，全く必要のないものです。
by Enrique (2011-01-18 10:23) 

>E#######
ぐへぇ！（驚）・・・こんなのが曲（楽譜）で表記されていたら嫌ですね（笑）、「これは一体何の嫌がらせだ！ o(T◇To)(oT◇T)oｲﾔｲﾔ!! （泣）」って感じで（爆）。　ただ、トリプルの♭だか♯だかは実際に表記された曲（楽譜）がある旨の記事をどこかで読んだ記憶があります。「正確な音程を出しなさい」って趣旨なのでしょうかね・・。

＞53ピタゴラス律と53平均律の誤差
　ここですが、５３ピタゴラス律はピタゴラス５度（３／２）を５３回積み重ねて（＆適宜ｎオクターブ下げて）作った音律、それに対して、53平均律は、１オクターブ（すなわち１２００セント）を５３で割って算出された音律という理解でよろしいでしょうか。
　mixiでマイミクの方から、５５等分律だと（３１を掛けることにより）純正５度近似の値が算出され、５３等分律だと（３２を掛けることにより）１／６ピタゴラスコンマ狭い５度に近似した値が算出される旨の意見が出まして、具体的には、
＞５３等分と５５等分は数字は近いですが傾向は全然違いますよ。
１２００÷５３×３１＝７０１．８８７セント　≒　純正完全五度
１２００÷５５×３２＝６９８．１８２セント　≒　純正完全五度－１／６Ｐ．Ｃ．

　という見解が出まして、思わず「おぉぉ、セント計算は、足し引き算だけでなく除／乗算も使えるのか！」と驚いた（＆目から鱗が落ちた）次第です。
　
　詳しくは、下記サイト（mixi日記のコメント欄）をどうぞ
http://mixi.jp/view_diary.pl?id=1644213391&owner_id=17562685

mixiにアクセス出来ない方で興味ある方は、下記サイトが参考になるかもしれません。ただ、下記記事で引用した「古楽の音律」の記述では、「５３分割法に基づくピュタゴラス音階」とか、「５３分割法に基づく純正律音階」、「５５分割法に基づく純正律音階」などと命名（？）されていて、何だか訳がわからない感もあります（汗）。
http://meantone.blog.so-net.ne.jp/2010-07-01
by koten (2011-01-18 12:45) 

kotenさん，nice&コメントありがとうございます。

ピタゴラス音律って原理が単純ですから，ちょこっとした計算面白いですね。
>E#######　≒　C
これ受けたみたいで，良かったです。ちょっと数えるの面倒でしたが。53平均律じたいは私が見た本にも出ていましたので，少し新奇性を出してみました。さすがに，それ以上はやる気が起きません。
＞５３ピタゴラス律はピタゴラス５度（３／２）を５３回積み重ね
＞53平均律は、１オクターブ（すなわち１２００セント）を５３で割って算出
全くその通りです。
55平均律っていうのも，確かにどこかで聞いたことがありますが，その方のご指摘通り音が多いのに，何がメリットなのか分かりません。5度が12平均律より悪く，長3度は少しいいものの，53平均律とは全く比べるものになりません。ピタゴラス式の計算ですと，53音の次は306音，その次が665音です。やみくもに細かく刻めばいいものではないことが分かります。例えば665音を666音にしただけで，精度がガタ落ちです。以下に，各種平均律のずれを示します。

　　　　　　　　　　長３度　　　　５度　　
１２平均律：　　+13.7　　　-2.0
５３平均律：　　-1.4　　　　　-0.07
５５平均律：　　+6.4　　　　-3.8
665平均律：　-0.15　　　　-0.00011

なお，平均律（均等律）は１オクターブを対数的に均等に分割する訳ですから，セントの計算とは分割数が違うだけで，同じことですね。「セントって平均律の子分のようなもの」と書きましたが，むしろセントって1200平均律ということで，同じものですよね。例えば上の665平均律の5度は，１オクターブを665個に分割した分の389個分ですから，1200分割した分のいくつ？と全く比例計算できるわけですね。ちなみに，665平均律は，いわばセント値の1200平均律よりも分割数少ないのに，ずっと性能が良いと思います。
もちろん，純正律などの比率，3/2，4/3，5/4など，本当の比率は，2の対数をとらないと，セントにのってきませんよね。
by Enrique (2011-01-18 20:45)