音律を考える(2) [音律]
前回,音律に関する(しないものもある),どうでもいい話を書きました。私自身平均律楽器を使い続けているため,具体例がなく説得力ありません。前回の結論めいたものとしては,音律に関する情報はやはり少ないこと,その原因の一つに,現在では音律研究は職業的研究テーマになりにくいので,音大のカリキュラムなどにものりにくいのではないかというものでした(調律師学校などではどうなんでしょうか)。
私自身音律にハマっているわけではないので,文献なども殆ど所持していません。しかし,kotenさんの記事では,分りやすい本が少なく,バイブル的なものは高値で取引されているのだそうです。そのような実態および前回の結論から浮かび上がってくるのは,過去の知識を分かりやすくまとめただけでは,一冊の本にはならず(もちろんそのような需要がモノスゴクあれば別でしょうが),著者独自の研究成果や主張も取り入れないと,マトモな本にならないという事情があるのではないでしょうか?それに,むしろ研究者としては,なるべく早く自説や自分の研究成果の方に持って行きたい。そうすると,ピタゴラス音律から始まる音律の基礎的なところは軽くすっ飛ばしたくなるのでしょう。そうすると,たとえば異名同音がどうなっているのか?異名異音の場合は#と♭の高低はどちらがどうなのか?とか,それはなぜか?といったような素朴な疑問が解決されないまま,著者の高尚?な自説や新しい試みなどに付き合わされる事になります。何もこの事は音律に限ったことでもないでしょうが。
それともうひとつ考えられる点としては,音律が数字やちょっとした計算を使う点です。いわば理系的でありながら芸術や美学と関わる点です。文系・理系と区別される日本では,どちらにも属さず抜け落ちてしまうキライもあるのかも知れません。音楽学専門の方はどうなのか知りませんが,一般音楽系の方はまず理系的でないと思われます。音大でも音響学などの理系的な科目は嫌われるようです。
音律の原理はシンプルといったのは,音律の基礎であるピタゴラス音律が純正5度(3/2倍)を12回繰り返した結果,7オクターブ上で元の音よりもやや行き過ぎてしまった音の高さであるピタゴラスコンマ(p.c., 24セントほど),もしくはピタゴラス音律の長3度の純正3度とのずれ(広い分)をいうシントニックコンマ(s.c., 22セントほど)を5度圏のどこにどう按分配置するかということに尽きるからです。
せいぜい指数の計算,セント値を使うにしても対数の計算が出来ればOKです。特に近代,音律研究をした学者たちの主な研究内容からしたら,全然メンドウなことはないのですが,かと言って音楽やるウチの妻に対数の計算ができる(というか考え方がわかる)かどうかはあまり自信ありません(多分ダメでしょう)。能力的問題というよりも,音楽芸術という深淵なものに対し理系的なものを浅薄なものだとみなす傾向もあるかもしれませんし,ただメンドウがキライなだけかもしれません。「誰かが美しく調律してくれたら弾くわ~」,と。
以下は音律に関する基本事項を書いているだけなので,分かっている方および興味ない方は読み飛ばしてもらってかまいません(つづく)。
上で使ったセントという単位は平均律の子分のような単位です。これを使う場合は対数の計算をしないといけません。理系の人間には何でもなくても,文系の人の多くには四則演算以外の計算は少し抵抗があるかもしれません。よく現代ギター誌などで,弦のピッチの正確さなどをこの単位で表しています。
1セントは1オクターブを平均律的に1200分割したものですので,音程の比率を底が2の対数を取り,1200倍した,
セント値 = 1200 log2(音程の比率)
で求められます。すなわち1オクターブ(音程2倍)は1200セントということで,純正5度は音程が3/2なので,701.955セント,純正長3度は音程が5/4なので,386.314セントとかと出ます。純正なのに半端な値が出るのは,セント値が平均律の計算方法だからで,平均律の音階がきちんとした値が出るようになっています。100セントが平均律の半音になるわけですね。対数をとった単位というのは理工学ではよくやることです。音や信号の強さのdB,化学のpH,地震の強さM,等々です。比率の桁数をとることになるので,掛け算割り算が足し算引き算に変換されることになるわけですね。
念のため,p.c.とs.c.のセント値を算出しておきましょう。
p.c.の比率は,もとの音からの12回目の5度回転(3/2)12の値の,もとの音(の何オクターブか上)に対する行きすぎ量です。これは7オクターブ上がっていますから,これを2の7乗で割れば,
(3/2)12/(27)=312/219=1.013643265
となります。これのセント値を上の式で求めれば,23.46セントほどになります。
s.c.の比率は,ピタゴラス音律の長3度の純正長3度からの高さですから,
(3/2)4/5=81/80=1.0125
ですね。これのセント値を同様に求めれば,21.51セントほどになります。
また,両者の2セント弱の差をスキスマとか言います。
ただし,セント値を明示的には使わなくても音律の議論は出来ます。
その場合は,p.c.やs.c.を単位にして,これらを何分割かして,やはり5度サークルのどこそこの5度間隔に割り振るかということです。ちなみに全ての五度間隔を1/12 p.c.にしたのが平均律ですね。ただ実際に比率を計算するには,n乗根(4分割なら4乗根,6分割なら6乗根など)を求めないといけません。
ミーントーン系では長3度を純正にとることが重視されますので,純正5度のみで組み立てたピタゴラス音律で生まれる広い長3度の純正長3度からのずれ(シントニックコンマ,s.c.)を単位に考えるようです。
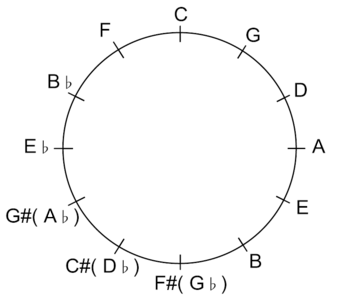
5度圏(サークル)図
これを使わなくても計算は出来ますが,直観的?に分かりやすいようです。本当は閉じません。でも良く出来たもので時計の文字盤と一緒です。通の人たちはこれを時計に例えて,何時と何時の間にp.c.やs.c.を何分割かして仕込むということを議論するようです。
音律の基礎ピタゴラス律では,Cからスタートして純正5度回転を12回繰り返すと元のCにほぼ戻りますが,上で書いたようにピタゴラスコンマ分通り過ぎてしまいますが,これを一致したことにすると,最後のF(正しくはE#)-C間の5度がp.c.分狭くなってしまいます(本当は右回り12回でB#=C+p.c.ということですね)これでは,ハ長調のIV和音が使えなくなってしまいますので,普通はこれを右回りと左回りから攻め,G#-E♭間にこの-p.c.を押し付けます。ここから様々な音律の魑魅魍魎が始まります。




>音楽芸術という深淵なものに対し理系的なものを浅薄なものだとみなす傾向もあるかもしれませんし
理系的なものを浅薄だとは思いません。
理系的なアプローチがまったくできませんのでコンプレックスです。
by Cecilia (2011-01-14 11:10)
Ceciliaさん,nice&コメントありがとうございます。
音律に関する議論は,特にそれがせめぎ合う所なんでしょうか?Ceciliaさんは決してそう言うことはないと思いますが,文系の方々の間には理系的なものに対する不理解(もちろんその逆)もあるように思います。文系・理系という分け方にも問題がありますし,とどめは「文高理低」なるヒドイ思想?も音律軽視の一因かもしれません。
by Enrique (2011-01-14 19:02)
音楽はもともと理系分野でしたよ。
ただ、音楽自体が独自に発展していったことによって
芸術分野のものとなったのです。
作曲家も演奏家も、既にある自分の「道具」に疑問を呈する暇はないですからね。
特に職業音楽家は、それだけそれぞれに高度な技能が求められるわけですし…。
もちろん作曲家の中には、様々な音律により作曲したり独自の楽器を開発したりする人もいますが。(ハリー・パーチやルー・ハリソン等)
例えば、ベートーヴェンやショパンのピアノ作品を眺めると
現代のピアノではうまく響かない、あるいは、野暮ったい響きになる和音の置き方が見られることがあります。
これは、当時の楽器と調律の特性によるものではないか、と私は考えています。
しかし、こういうこと(現象)は、現代では少し難しいかもしれません。
前述のパーチやハリソンも、どちらかと言うと、音楽史の中では異端的な存在として受け止められてしまうことが多いのではないのでしょうか…。
これは、音楽家の怠惰と言うことよりも、社会の在り方に因る、のではないでしょうか。
何故なら、音楽は、芸術であると同時に、仕事でもあり趣味でもあるからです。
つまり、現代の、需要供給の関係を極端に重視する経済志向の世の中が
(西洋音楽の場合)この現代の一般的な音楽の状態を欲しているのではないかと思うのです。
by 通りすがり (2011-01-15 01:44)
通りすがりさん,コメントありがとうございます。
そうですね。科学と芸術の分化は案外最近のことのようですね。ごく絞って言えば,演奏家が音程を作れる楽器はまだしも,鍵盤楽器などでは演奏家と調律家の分化があるわけですね。
ご案内のハリー・パーチやルー・ハリソン等は,旧来の楽器に飽き足らず,音律面から洗い直したわけで,音楽自体は聞いたこと無いですが,すぐれた業績だとは思いますね(ジョン・ケージとかは,音楽としては分りませんが)。
ベートーベンはもちろんのこと,時代を下ったショパンでさえも,例えばむしろ純正律に近いキルンベルガー第1に合うなどというのは驚くべきことですね(でもないのかもしれないですが)。プレイエルのピアノが合うなどというのは,音色やアクションもさる事ながら調律もポイントだったのかもしれませんね。
平均律を使った現代の楽器の音色・音質をうるさいこと言っても,たかが知れているような気がしますが,楽器の値段などは音律とは別のところに求められるようです。
音楽家は食べていかなければならないので,音律面のアレコレはむしろ趣味のしろうと分野(古楽の調律家などは別として)と言うことになるかもしれないですね。
>需要供給の関係を極端に重視する経済志向
これが職業的音楽家の活動を規制してしまっていますね。無理も無いことです。
by Enrique (2011-01-15 08:26)